Howto program Hanoi statefree
[from a pattern-based perspective]

Well it would be more convinient with a function f where
N is the number of rings
n is a counter for the total moves that is (N^2 -1)
nActual = current position in the sequence.
0............nActual..........n = (N^2)-1.
We always step 1 step forward and the game's start-position is represented by 0.
The start position is represented by the number 0.
Then nActual increase with 1
and continue forward until nActual becomes n= (N^2)-1.

Whatever value nActual hold in the range 1 to (N^2)-1
we can use as argument to f(nActual) and have f return the move between.
the previous position [ nActual -1 ] and [ nActual ] itself.
So far so good.

So Lets start looking for some patterns.

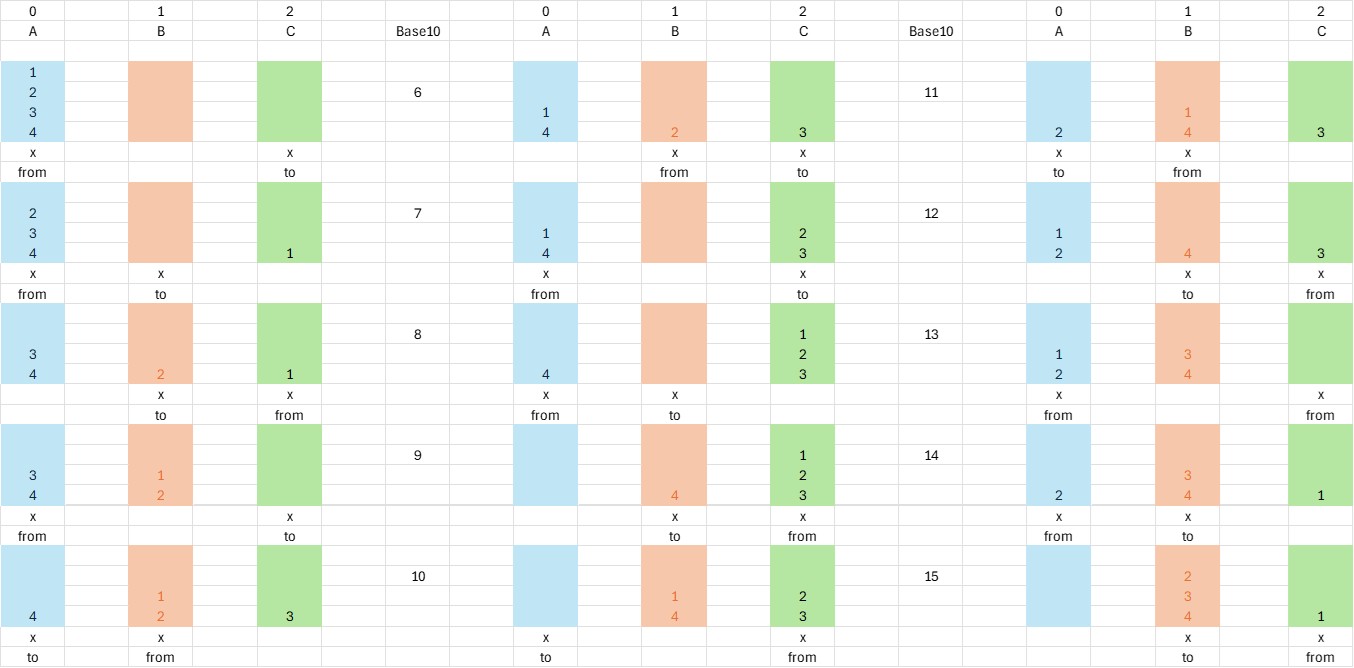
Look at the depiction above. Here we have 4 rings to start with.

We observe a pattern of repititious movements
the 2 [x]'s under each colorblock suggests witch 2 poles
that are interrelated to moves. It goes A->C, A->B, C->B. A->C, B->A ....
But wait a minute. How can we predict anything about the [ from -> to ] set.
Notice! The first 4 [from to movements] describes a pattern.
From A->C and so on, But the 5. B->A breaks the
pattern!. Should have been A->B Like the 2. move was! Although the pattern of [x]'s under the blocks is consistent
The direction isn't. So we cant predict! We only observe it!. Not calculate it!
Later the pattern of [x]'s will return with a vengance

But for now lets consider some likely candidates for becoming numbers to represent nActual.
We know Base10 number system, but lets move down
to examine Base3 since there are 3 poles
Base2 since we move between 2 poles
Base1 to tell us if we get more information the lower the Base is.

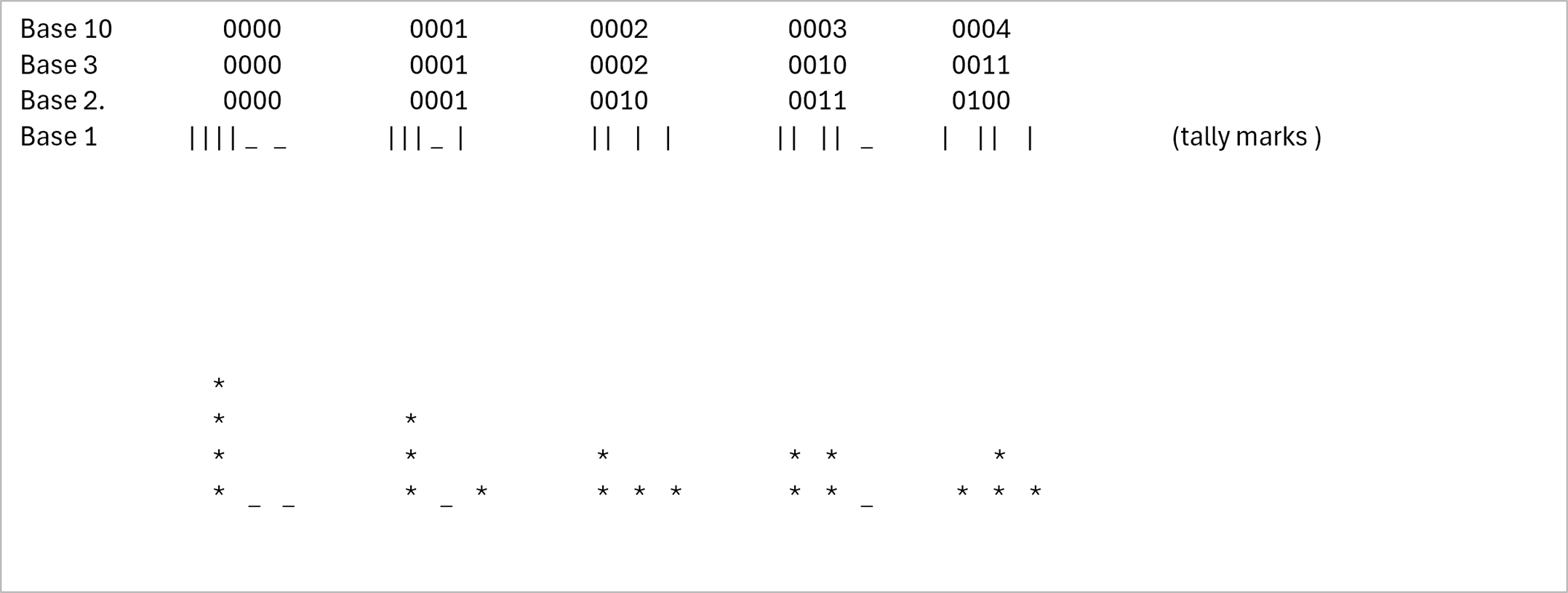
First attempt!.Look at the depiction above. Here we have 4 different base number systems.
The * represent the rings and their current pole-position.


We can see the Base 1 describes the rings position. But what is the serial progression ?
The way the tally marks are arraged here actualy depicts the position in itself.
And thus give us direction directly in comparison
That contradicts the intent to investigate for lower complexity with lower base. Can you see why ?.
It is because the tally marks in this configuration actually ia a Base 16 number.
Base 16 in this tally mark form hold the solution in itself for N = 4. But not for another N. This way of finding a pattern is quickly
becoming impossible with increasing N
If N were 100 we would have to know a numbersystem with 10000 signs reperesenting 1 ... 10000.
We will get back to this later, when we look for a posible mathematical solution.
In short!, Base 1 number progression is hard to remember and unsuitable for pattern recognition

Base 10 have a progressive forward moving pattern. 1,2,3,.. and so on
But give us not enough translatable information on positions.
Base 3 have a progressive forward moving pattern 0000,0001,0002,0010,0011 .. etc.
But the 0's in base 3 do not accurately describe the number of rings on the initial A pole
as Base 2 does. Base 2 have a wellknown progressive forward moving pattern 000,001,010,011 .. etc.
And indicate positions that possibly can be translated .
the initial 0 ,0 , 0, 0 , would then have to indicate 4 *'s on the A position.
The Base 2 leftmost 0's have a pattern of precisely counting the number of rings on A.
That is enough for us to look further into Base 2.

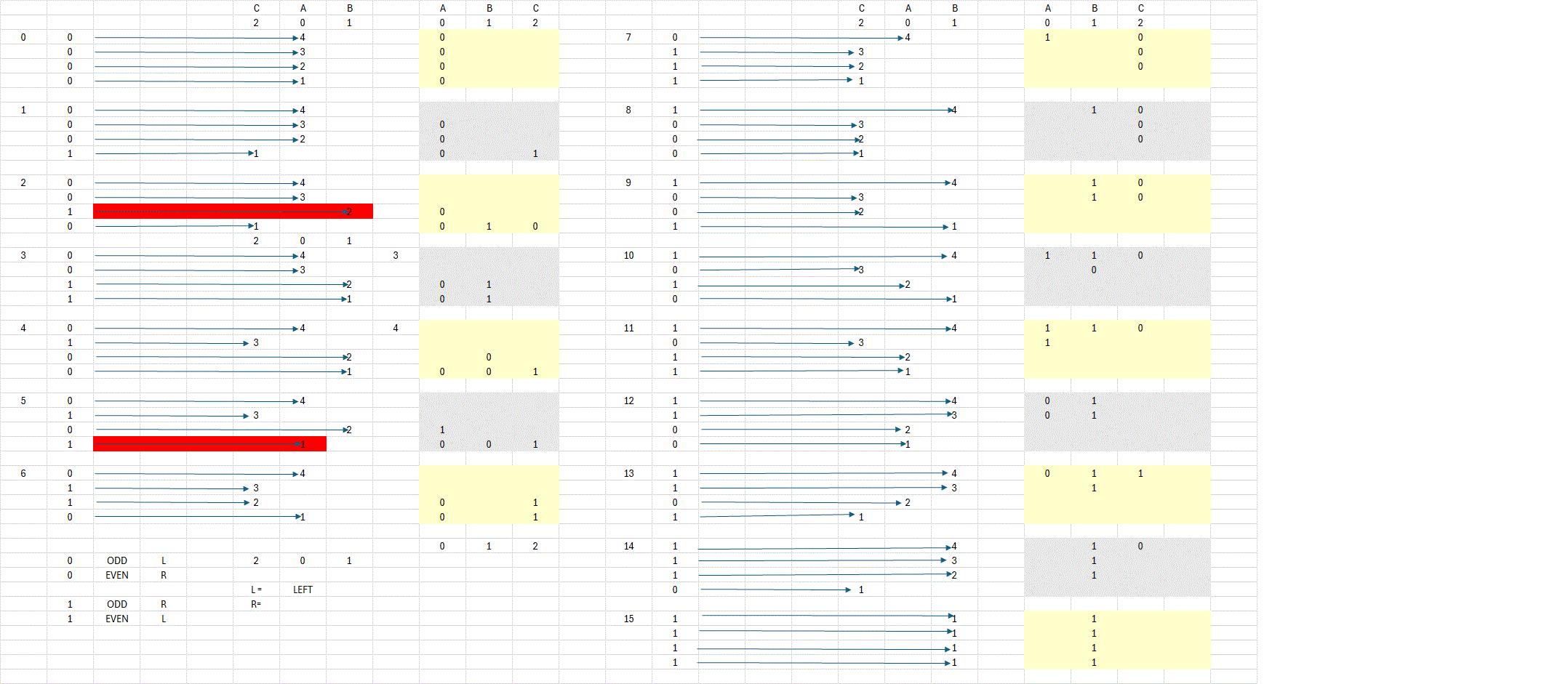
Here in this arrow diagram we see the movements more clear.
The arrows marked with red indicate where the pattern break.
The AC,AB,CB,AC direction folows a pattern but the ... BA breaks it. Also the ODD and EVEN indications attempt to see if the number nActual in itself hold any info on the direction. There are none. But remember we allready established that f(nActual) will have to look at [nActual] compared to the previous [nActual-1]. So lets move on and compare those up against eatchother.

Here we anotate- with yellow color - the known [ from ] number pattern from the topmost image
and search for patterns between [nActual-1] and nActual. We observe that the 1. 2. 4. and 8. move hold no opposite positioned 1's.
In addition they all start [from 0]. Other start from 0 too. They are 7,13 and 14.
So what patterns do we observe in [nActual] being 7, 13 and 14 ?.
in 7 the green anotated numbers yields 6. In modulus 3 that means 0. 6%3 = 0.
13 and 14 in the green anotated area yields 12. Also 0 in modulus 3. 12%3=0.
The [ From 1 ] pattern occur in 5, 6 and 11.
where 5 and 6 green anotated area with opposit placed 1's yield 4. 4%3=1.
[nActual] with modulus 3 we get a consistent pattern where to move from.